สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
แอดมินต้องขอโทษเพื่อนๆ ด้วยนะครับ วันนี้เพิ่งเลิกเรียนในวิชา ENERGY METHODS IN APPLIED MECHANICS เลยมาพบกันช้าไปสักหน่อย วันนี้ผมจะมาแสดงขั้นตอนในการคำนวณหาค่าการเสียรูปในโครงสร้างที่มีหน้าตัดเป็นแบบ CRACKED SECTION ตามที่ผมได้รับปากเพื่อนๆ เอาไว้นะครับ โดยผมคิดว่าวิธีการที่ดีที่สุดก็คือสมมติปัญหาขึ้นมาและทำให้เพื่อนๆ ได้ดูจะเป็นการดีที่สุดครับ
ปัญหามีอยู่ว่า เราต้องทำการออกแบบหน้าตัดคาน คสล หนึ่งคาน เป็นคานช่วงเดียว ความยาวคานเท่ากับ 8 ม
เราจะใช้กำลังวัสดุเป็นคอนกรีตที่มีค่า fc’ เท่ากับ 210 ksc ค่า fy ของเหล้กเท่ากับ 4,000 ksc
รับ นน บรรทุกแบบจุดใช้งานเท่ากับ 3,000 kgf และเมื่อแปลงให้เป็น นน บรรทุกแบบเพิ่มค่าๆ นี้จะมีเท่ากับ 4,800 kgf
จงหาค่าการเสียรูปแบบทันทีทัยใดที่เกิดขึ้นของคานๆ นี้
ก่อนอื่นเราจะทำการการหาขนาดความลึกของหน้าตัดที่เล็กที่สุดตามที่ CODE ระบุจะได้ว่า
T min = L/16 = 8/16 = 0.50 m
ผมจึงกำหนดให้ใช้ค่าความลึกเท่ากับ 0.60 m ซึ่งจะมากกว่าค่าขั้นต่ำที่คำนวณได้
ความกว้างของคานใช้เท่ากับ
B = T/3 = 0.6/3 = 0.20 m
ดังนั้นคานเราจึงมีค่าโมเมนต์ความเฉื่อยของหน้าตัด UNCRACKED SECTION เท่ากับ
Ig = (0.2)(0.6)^(3)/(12) = 0.0036 m^(4)
สมมติค่าโมดูลัสยืดหยุ่นของคอนกรีตเท่ากับ
E = 2×10^(5) ksc = 2×10^(9) kgf/m^(2)
หากเราทำการวิเคราะห์โครงสร้างจะพบว่าหน้าตัดจะมีค่าโมเมนต์ใช้งานเท่ากับ
Ma = Ps L / 4 = (3,000)(8)/(4) = 6,000 kgf-m
และมีค่าโมเมนต์ดัดแบบเพิ่มค่าเท่ากับ
Mu = Pu L / 4 = (4,800)(8)/(4) = 9,600 kgf-m
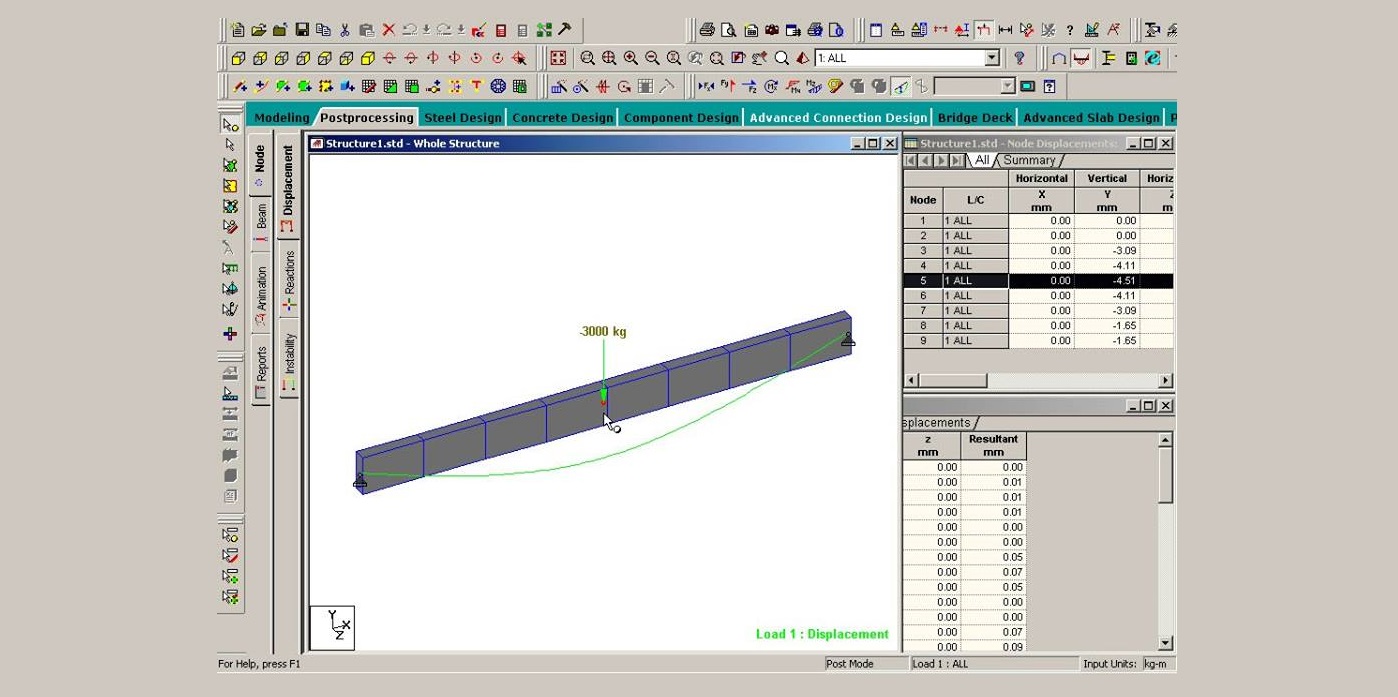
หากเราทำการวิเคราะห์หาค่าการเสียรูปจากหน้าตัดแบบ UNCRACKED SECTION (ดูรูปที่ 1 ประกอบ) หรือ อาจจะคำนวณค่าการเสียรูปนี้จาก EXACT EQUATION จะพบว่ามีค่าเท่ากับ
Δ = Ps L^(3) / (48 EI) = (3,000)(8)^(3) / (48)[2×10^(9)](0.0036) = 0.0045 m = 4.5 mm
หากทำการตรวจสอบค่าการโก่งตัวที่ยอมให้จะพบว่าม่ค่าเท่ากับ
Δa = L/360 = 8,000/360 = 22 mm
ซึ่งจะมีค่ามากกว่าค่าที่เกิดขึ้นจริงค่อนข้างมากนะครับ
ต่อมาเราจะทำการวิเคราะห์หน้าตัดแบบที่เป็น CRACKED SECTION กันบ้างนะครับ
เริ่มจากเราต้องทำการออกแบบเหล็กเสริมก่อนนะครับ ในเมื่อ Mu = 9,600 kgf-m
ค่า β1 = 0.85
ค่า m = fy/0.85fc’ = 4,000/(0.85×210) = 22.41
ค่า Pb = 6120β1/(6120+fy)m
Pb = 6120×0.85/(6120+4000)(22.41) = 0.0228
กำหนดให้ค่า Pmax = 0.5Pb = 0.0114
ค่า Pmin = 14/fy
Pmin = 14/4,000 = 0.0035
ค่า b = 20 cm
ค่า d ~ 0.55 cm
ดังนั้นคานจะต้องการอัตรส่วนเหล็กเสริมเท่ากับ
P req’d = 1/m(1-SQRT(1-2mMu/[Øbd^(2)fy]))
P req’d = 1/22.41(1-SQRT(1-2 x 22.41 x 9,600 x 100 / ( 0.9 x 20 x 55^(2) x 4,000))) = 0.0046
ดังนั้นค่า Pmin < P req’d < Pmax ถือว่าสามารถใช้ค่านี้ได้
As = P req’d b d = 5.104 cm^(2)
ใช้เหล็กรับแรงดึงเท่ากับ 2DB20mm มี As = 3.14×2 = 6.28 cm^(2)
ใช้เหล็กรับแรงอัด (ถึงแม้ว่าหน้าตัดจะไม่ต้องการก็ตาม แต่ ไม่ว่าอย่างไร เราก็จำเป็นต้องใส่อยู่แล้วเพื่อที่จะทำการยึดเหล็กปลอก) เท่ากับ 2DB12mm มี As’ = 1.13×2 = 2.26 cm^(2)
ต่อมาผมทำการแบ่งช่วงคานออกเป็นทุกๆ ระยะ 1 ม และ ทำการหาค่าโมเมนต์ใช้งานเฉลี่ยจากแต่ละช่วงจะได้ว่า
ช่วงที่ 0-1 m และ 7-8 m ค่าโมเมนต์ใช้งานเฉลี่ยจะเท่ากับ
Ma = (0+1,500)/2 = 750 kgf-m
ช่วงที่ 1-2 m และ 6-7 m ค่าโมเมนต์ใช้งานเฉลี่ยจะเท่ากับ
Ma = (1,500+3,000)/2 = 2,250 kgf-m
ช่วงที่ 2-3 m และ 5-6 m ค่าโมเมนต์ใช้งานเฉลี่ยจะเท่ากับ
Ma = (3,000+4,500)/2 = 3,750 kgf-m
ช่วงที่ 3-4 m และ 4-5 m ค่าโมเมนต์ใช้งานเฉลี่ยจะเท่ากับ
Ma = (4,500+6,000)/2 = 5,250 kgf-m
สรุปเราจะได้ค่า Ma ในคานนี้เท่ากับ 4 ค่านะครับ
ผลจากการวิเคราะห์หน้าตัดจะพบว่าค่า Mcr = 3,480 kgf-m
โดยที่ค่า Icr = 0.00125158 m^(4)
ดังนั้นที่หน้าตัดซึ่งมีค่า Ma < Mcr เราจะสามารถใช้ค่า I eff = Ig ได้เลยนะครับ
เนื่องจากการคำนวณค่า I eff นั้นสามารถทำได้นะครับ แต่ จะมีความยุ่งยากมากพอสมควร ผมจึงเขียนโปรแกรมในการคำนวณหาไว้ในเครื่องคิดเลข TI-92 Plus ของผมเพื่อที่จะคำนวรได้เร็ว
โดยที่ค่า I = bh^(3)/12
ดังนั้น
b = (12)(I eff)/h^(3) = (12)(I eff)/0.6^(3) = 55.56(I eff)
ค่า I eff สำหรับ ช่วงที่ 1 และ 2 ค่า I eff = Ig = 0.0036 m^(4)
ค่า b = 55.56(0.0036) = 0.20 m (เท่าเดิม)
ค่า I eff สำหรับ ช่วงที่ 3 ค่า I eff = 0.0031245 m^(4) < Ig
ค่า b = 55.56(0.0031245) = 0.174 m (ลดลงจากเดิม)
ค่า I eff สำหรับ ช่วงที่ 4 ค่า I eff = 0.00193413 m^(4) < Ig
ค่า b = 55.56(0.00193413) = 0.107 m (ลดลงจากเดิม)
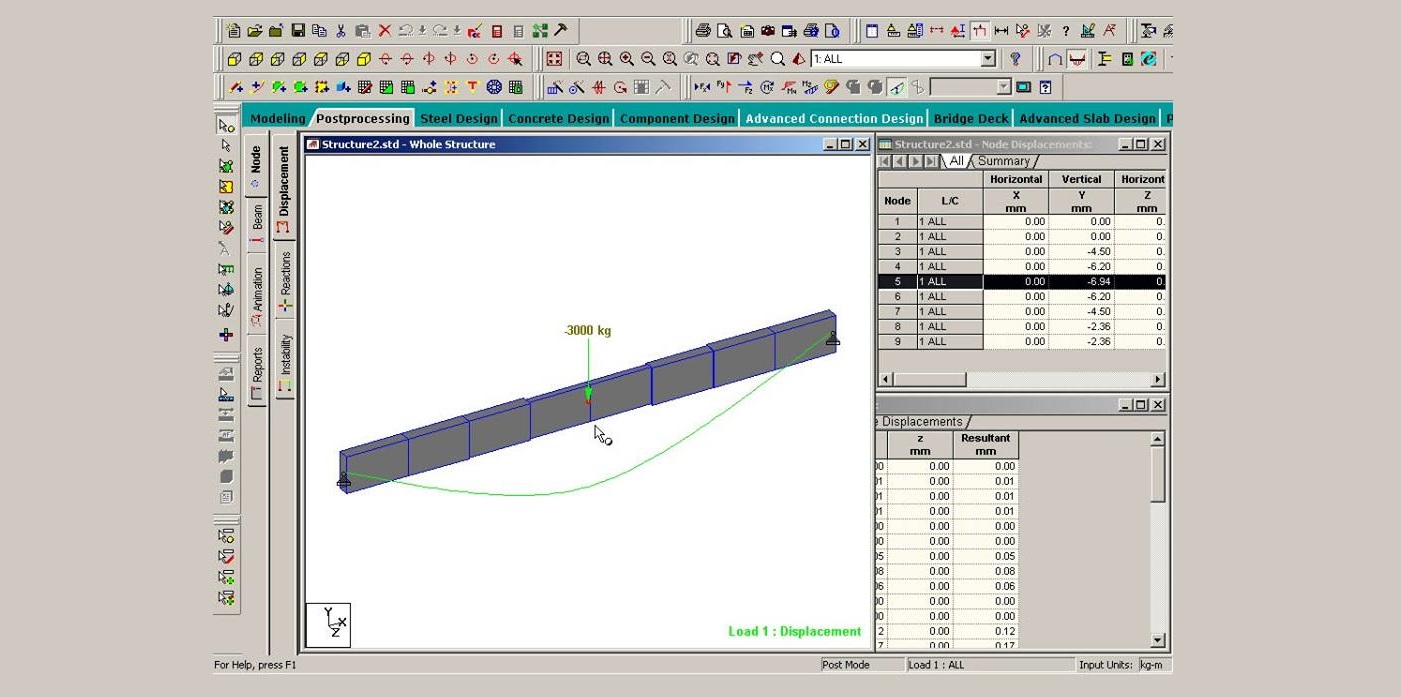
หากเราทำการวิเคราะห์โครงสร้างใหม่ (ดูรูปที่ 2) โดยใช้ค่าคุณสมบัติต่างๆ ข้างต้นจะได้ค่าการเสียรูปใหม่เท่ากับ
Δ = 6.94 mm > 4.5 mm
จะพบว่าค่าการเสียรูปจะเพิ่มขึ้นมากกว่าการที่เราใช้ค่า Ig ในการคำนวณ แต่ จะยังน้อยกว่าค่าที่ยอมให้อยุ่มากนะครับ
ต่อมาหากเราจะใช้ข้อกำหนดของ มยผ ซึ่งระบุไว้ว่าให้ใช้ค่า I eff ในคานเท่ากับ 0.35 Ig = 0.35×0.0036 = 0.00126 m^(4)
ค่าการเสียรูปใหม่จะมีค่าเท่ากับ
Δ = Ps L^(3) / (48 EI) = (3,000)(8)^(3) / (48)[2×10^(9)](0.00126) = 0.015 m = 15 mm
จะพบว่าค่าการเสียรูปจะเพิ่มขึ้นมากกว่าการที่เราใช้ค่า Ig และ I eff ในการคำนวณ แต่ ก็จะยังน้อยกว่าค่าที่ยอมให้อยู่นะครับ
เพื่อนๆ จะเห็นได้ว่าขั้นตอนที่ผมทำให้ดูนั้นเพื่อนๆ สามารถที่จะทำได้นะครับ แต่ อาจจะยุ่งยากและใช้เวลาสักหน่อย ครั้นจะใช้ค่าโดยประมาณตามที่ได้แนะนำไว้โดย มยผ ก็จะให้ค่าที่ไม่ประหยัดสักเท่าไหร่
ดังนั้นหากเราทำตามข้อกำหนดที่ CODE การออกแบบระบุให้ใช้เราก็มักไม่ต้องกังวลถึงเรื่องการแอ่นตัวของโครงสร้างนะครับ ยกเว้น หากเราต้องทำการคำนวณออกแบบในกรณีที่คานของเรานั้นต้องรับ นน บรรทุกที่มากกว่าปกติ เราอาจต้องนำวิธีการนี้มาใช้นะครับ
วันพรู่งนี้ผมจะนำภาพในโปรแกรมในเครื่อง TI-92 Plus มาอธิบายทีละขั้นตอยในการ INPUT และรับ OUTPUT ออกมา เพื่อนๆ จะได้เข้าใจกระบวนการในการคำนวณมากยิ่งขึ้นนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN