การคำนวณหาสถานะของความสมดุล (STAGE OF EQUILIBRIUM) ในโครงสร้าง
สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
วันนี้ผมจะขอมายก ตย ในการคำนวณหาสถานะของความสมดุล (STAGE OF EQUILIBRIUM) ในโครงสร้างตามที่ได้เคยรับปากกับเพื่อนๆ เอาไว้เมื่อวานนะครับ
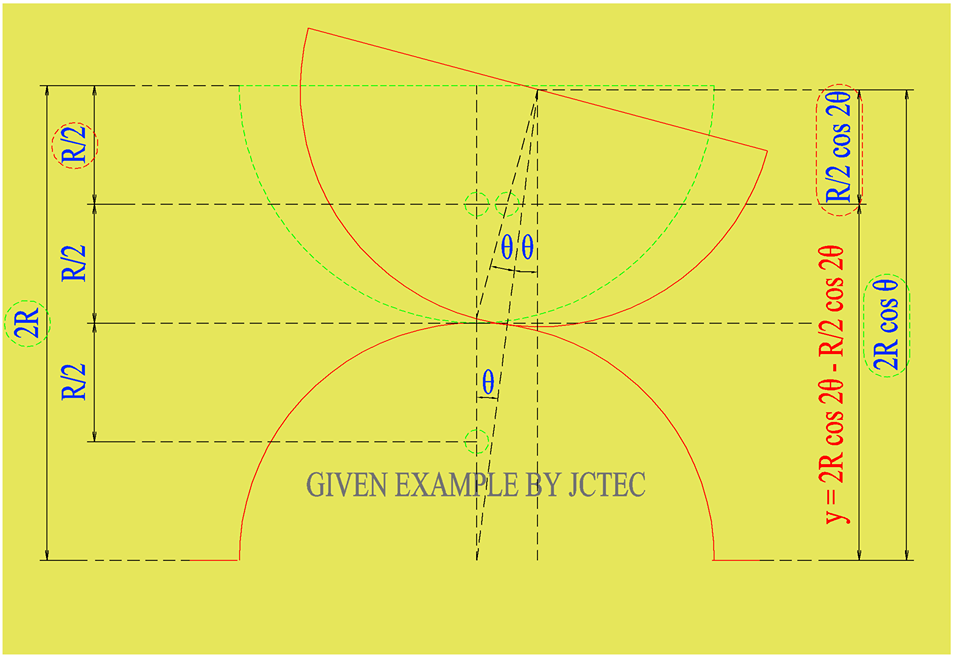
เริ่มต้นดูจากในรูปก่อนนะครับ ในรูปเป็นโครงสร้าง SHELL รูปครึ่งวงกลมวางซ้อนกันอยู่ 2 อัน โดยหากดูรูปในเส้นประสีเขียวจะพบว่า ณ จุดๆ นี้ คือ ตำแหน่งดั้งเดิมของมัน ก่อนที่จะเกิดการหมุนตัวไปเท่ากับมุม θ ซึ่งหมายความว่าหากก่อนการหมุนค่ามุม θ จะเท่ากับ 0 ดังนั้นหากไม่มีแรงกระทำใดๆ มาผลักหรือหมุน SHELL นี้ สภาวะของความสมดุลของ SHELL นี้ก็จะอยู่ในสภาวะที่เรียกว่าสมดุลสะเทิน หรือ ผลจากการ PARTIAL DIFFERENTIATE ไม่ว่าจะสักกี่ ORDER ก็ตามก็จะออกมาเท่ากับ 0 หรืออาจเขียนได้ว่า
∂^(n)V / ∂θ^(n) = …… = ∂^(∞)V / ∂θ^(∞) = 0 (เมื่อแทนค่าให้ θ = 0)
มาดูกันต่อนะครับ ก่อนการหมุนระยะในสมการ y จะมีค่าเท่ากับ
y = 2r – r/2 = 3r/2
แต่เมื่อใดก็ตามที่เกิดการหมุนจนทำให้เกิดมุม θ นั้นเกิดขึ้นในตัว SHELL นี้จะพบว่าระยะในสมการ y จะลดลงไปจากเดิมเป็น
y = 2 r cos (θ) – r/2 cos (2θ)
ซึ่งในสมการๆ นี้ค่า θ ก็คือตัวแปรที่เราให้เป็น GENERALIZED COORDINATE นั่นเองครับ
มาเริ่มต้น PARTIAL DIFFERENTIATE กันใน 1ST ORDER กันนะครับ
∂V / ∂θ = -2 r sin (θ) + r sin (2θ) = 0
ต่อด้วยการ PARTIAL DIFFERENTIATE กันใน 2ND ORDER กันนะครับ
∂^(2)V / ∂θ^(2) = -2 r cos (θ) + 2 r cos (2θ) = 0
ในขั้นตอนนี้เองครับ หากเรา SET คำตอบของสมการให้เท่ากับ 0 เราจะสามารถแก้สมการหาคำตอบของตัวแปร GENERALIZED COORDINATE ที่จะทำให้โครงสร้างนี้สมดุลได้นั่นเอง
โดยหากเพื่อนๆ ลองแก้สมการเหล่านี้ดูจะพบว่าค่า θ ทีไ่ด้ออกมานั้นจะมีหลายคำตอบมาก ซึ่งแน่นอนที่สุดเราจะเลือกค่าของคำตอบที่มีค่าน้อยที่สุดเพื่อเป็นคำตอบของมุม θ ที่สามารถเกิดขึ้นได้ในโครงสร้างของเรา
ต่อด้วยการ PARTIAL DIFFERENTIATE กันใน 3RD ORDER กันนะครับ
∂^(3)V / ∂θ^(3) = 2 r sin (θ) – 4 r sin (2θ) = 0 (เมื่อแทนค่าให้ θ = 0)
ต่อด้วยการ PARTIAL DIFFERENTIATE กันใน 4TH ORDER กันนะครับ
∂^(4)V / ∂θ^(4) = 2 r cos (θ) – 8 r cos (2θ) = -6r < 0 (เมื่อแทนค่าให้ θ = 0)
เพื่อนๆ เห็นคำตอบในการ PARTIAL DERIVATIVE นี้ใช่มั้ยครับ คำตอบที่ออกมามีค่าเท่ากับ -6r ซึ่งจะน้อยกว่า 0 ดังนั้นโครงสร้าง SHELL เมื่อต้องวางตัวอยู่ในระนาบมุม θ ใดๆ ถึงจะทำให้มุมๆ นี้อยู่ในค่าๆ หนึ่งที่จะทำให้โครงสร้างทั้งระบบอยู่ในสมดุล (EQUILIBRIUM) ได้ แต่ สถานะของความสมดุล (EQUILIBRIUM STAGE) นี้ก็ยังถือว่าเป็นแบบไม่เสถียร (UNSTABLE) อยู่ดีครับ
ก็หวังว่าเพื่อนๆ จะพอเข้าใจถึงการนำหลักการ ENERGY METHODS ที่ผมนำมาเล่านี้ไปใช้ในการประยุกต์ในการตรวจสอบสถานะของความสมดุลในโครงสร้างที่เพื่อนๆ อาจจะต้องมีส่วนเกี่ยวข้องอยู่ได้นะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN
Bhumisiam ภูมิสยาม
ผู้ผลิตรายแรก Spun MicroPile
1) ได้รับการรับรองระบบการจัดการอาชีวอนามัยและความปลอดภัย ตามมาตรฐาน ISO 45001:2018
2) ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐาน ISO 9001:2015
3) ได้รับมาตรฐาน ISO 9001:2015 UKAS ภายใต้การดูแลของ อังกฤษ
4) ได้รับมาตรฐาน ISO 9001:2015 NAC ภายใต้การดูแลของ สำนักงานมาตรฐานผลิตภัณฑ์อุตสาหกรรม
5) ได้รับมาตรฐาน มอก. 397-2524 เสาเข็ม Spun MicroPile Dia 21, 25, 30 cm.
6) ผู้ผลิต Spun MicroPile ที่ได้รับ Endorsed Brand รับรองคุณภาพมาตรฐานจาก SCG
7) ผู้นำระบบ Computer ที่ทันสมัยผลิต เสาเข็ม Spun MicroPile
8) ลิขสิทธิ์เสาเข็ม Spun MicroPile
9) เทคโนโลยีการผลิต จากประเทศเยอรมัน
10) ผู้ผลิต Spun MicroPile แบบ “สี่เหลี่ยม”
11) การผลิตคอนกรีตและส่วนผสม ใช้ Program SCG-CPAC
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-50 ตัน/ต้น ขึ้นอยู่กับสภาพชั้นดินแต่ละพื้นที่
5) สามารถตอกชิดกำแพง ไม่ก่อให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็มสปันไมโครไพล์ มาตรฐาน มอก. โทร
☎ 082-790-1447
☎ 082-790-1448
☎ 082-790-1449
☎ 081-634-6586